Section 2.3 - Functions
Section Objectives
- Determine whether a relation is a function.
- Determine the domain and range of a function.
- Use function notation and evaluate functions.
- Interpret graphs of functions. Find and use the intercepts of the graph of a function.
- Simplify difference quotients.
Relations
A relation is a set of ordered pairs.
Any set of ordered pairs automatically relates the set of first coordinates to the set of second coordinates. The domain of a relation is the set of all first coordinates. The range of a relation is the set of all second coordinates.
Examples
- Consider the relation defined by . What is the domain? What is the range? Can you think of a formula that describes the relation?
- Consider the relation defined by . What is the domain? What is the range?
- If variables are used as symbols to represent the coordinates, we often use for the 1st coordinate and for the 2nd coordinate. You are probably already used to this idea. Now consider the relation .
The graph of a relation involving real numbers is the collection of all ordered pairs plotted in the rectangular (Cartesian) coordinate system.
- Look back at the previous examples, and sketch the graphs of the relations.
Functions
A function is a relation in which every element of the domain is paired with exactly one element of the range.
Equivalently, a function is a relation in which no two distinct ordered pairs have the same first coordinates. (2nd coordinates can be reused, but 1st coordinates cannot!)
Functions (and relations) are typically defined in one of four ways:
- Table or list
- Graph
- Formula, equation, or function notation
- Verbal description
Vertical Line Test: If a relation can be graphed in the rectangular coordinate system, the relation is a function if and only if no vertical line passes through the graph more than once.
If even one vertical line intersects the graph two or more times, the graph is not the graph of a function.
Function Notation
In this course, the most common way in which a function will be defined is by a formula or equation.
For example...
Consider the function .
This function can be described in an equivalent way by the formula: .
In this context, the free input variable is the independent variable and the output variable is the dependent variable.
In functional notation, we name the function (rather than the dependent variable) and describe the relation: .
is the value of the function named when evaluated at the input value . It is often read " of " or " at ."
Examples
- Sketch the graph of the function defined above.
- Let for any real number, . Evaluate . What does the graph of look like? How do we know defines a function?
VERY IMPORTANT IDEA: When the domain of a function is not explicitly stated, we assume the domain is the largest set of real numbers that produce valid, real outputs from the function's definition. In this case, the domain is sometimes called the implied domain.
- What is the domain and range of the function ?
- What is the domain of the function ?
Let .
- Does this actually define a function?
- What is the domain of ?
- Evaluate .
- Find the - and -intercepts of the graph of .
- Evaluate .
- Evaluate and expand .
Consider the relation whose graph is shown below. Let's call it .
- Is this the graph of a function?
- What is the domain of ?
- What is the range of ?
- Evaluate , , , .
- Find the - and -intercepts.
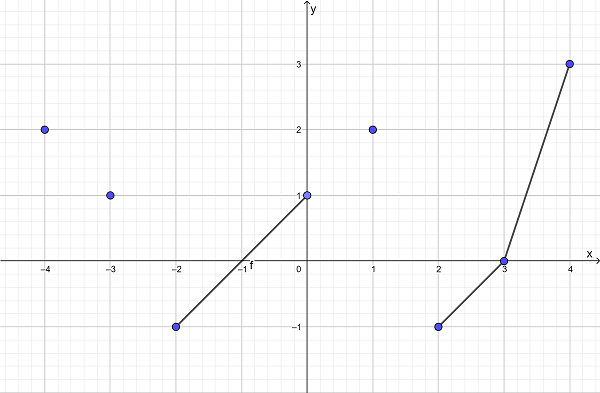
Let .
- Evaluate .
- Evaluate and expand .
- Evaluate and expand .
- Evaluate, expand, and simplify the difference quotient .