Sections 2.6 - Graphing Special Parabolas
Section Objectives
- Graph parabolas whose equations have the form .
- Graph parabolas whose equations have the form .
Parabolas
The graph of a quadratic equation of the form is called a parabola. Parabolas are examples of more general conic sections. A parabola is a smooth U-shaped curve. The turning point of the U is called the vertex, and parabolas are symmetric about the line through the vertex.
The parabola described by is a graph you should become familiar with. The graph is a smooth U shape, opening upward, with its vertex at .
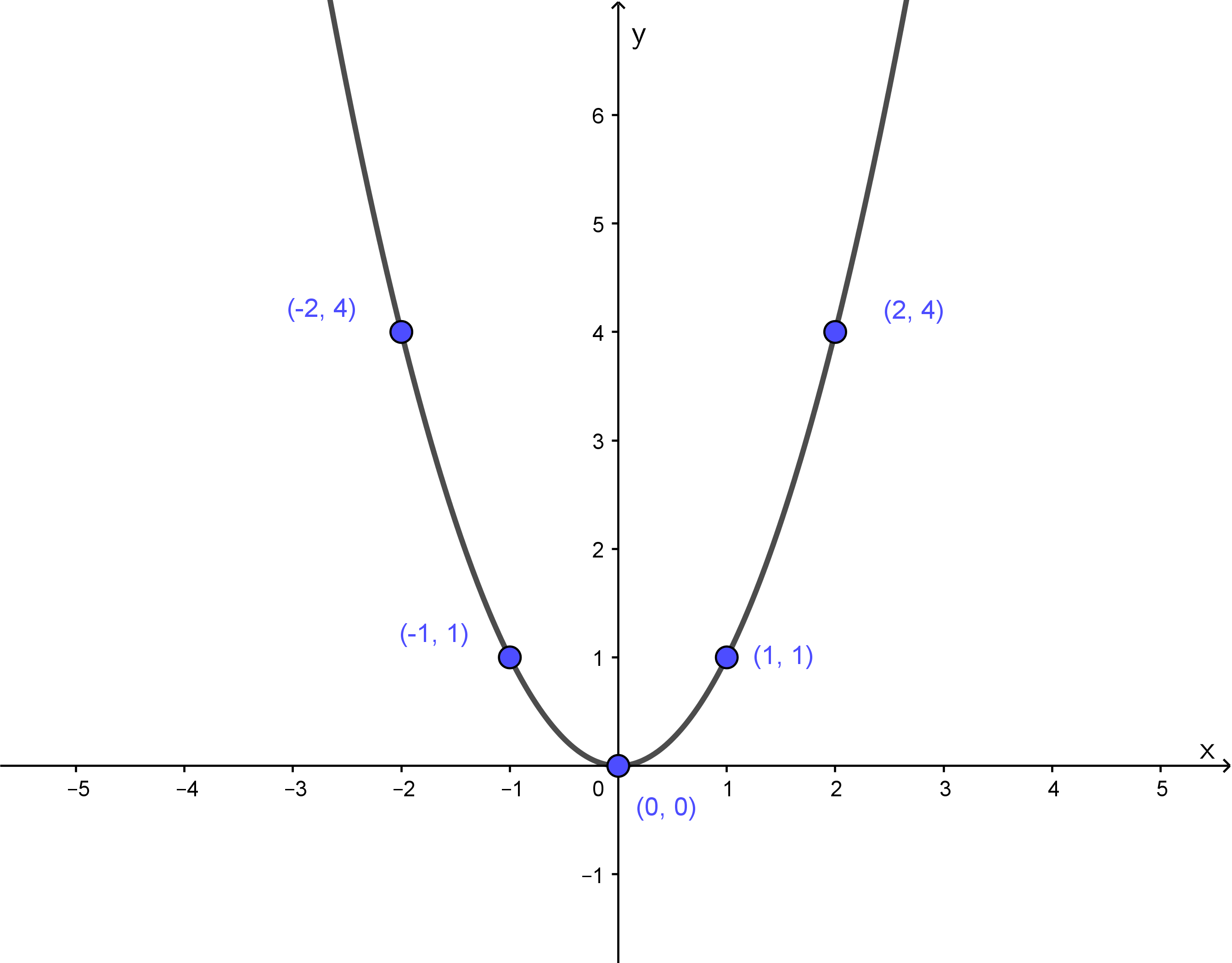
The standard parabola can be transformed in a number of ways:
- The graph of is flipped about the -axis.
- The graph of with is vertically stretched.
- The graph of with is vertically compressed.
- The graph of is shifted up or down depending on the sign of . The vertex is at .
By thinking about these transformations and plotting a few points, it is easy to graph basic parabolas.
Examples
- Consider the parabola described by . Make a table of points satisfying the equation and sketch the graph.
- Consider the parabola described by . Make a table of points satisfying the equation and sketch the graph.
- Consider the parabola described by . Make a table of points satisfying the equation and sketch the graph.