Section 2.7 - Analyzing Graphs
Section Objectives
- Given the graph of a function, determine where the function is positive, negative, or zero.
- Given the graph of a function, determine intervals on which the function is increasing, decreasing, or constant.
- Given the graph of a function, determine the local maxima and minima.
Analyzing Graphs of Functions
A common technique for determining information about a function is to draw conclusions from its graph. However, once you learn calculus, graphical techniques will probably become less popular.
Before we begin, recall that the graph of a function passes the vertical line test--any vertical line crosses the graph of a function at most once.
Important definitions
A function is increasing on any interval where greater -values give greater function values. On such an interval, the graph moves upward to the right.
A function is decreasing on any interval where greater -values give lesser function values. On such an interval, the graph moves downward to the right.
If the function values do not change on an interval, the function is constant. On such an interval, the graph is flat (horizontal).
A local (relative) maximum value is a function value that is greater than all function values on a surrounding open interval. Maxima appear on graphs at high points.
A local (relative) minimum value is a function value that is less than all function values on a surrounding open interval. Minima appear on graphs at low points.
A function is even if , that is to say, the replacement of by results in the original function. The graph of an even function is symmetric about the -axis.
A function is odd if , that is to say, the replacement of by results in the opposite of the original function. The graph of an odd function is symmetric about the origin.
Examples
- Sketch the graph of . Determine open intervals on which is increasing/decreasing. Determine any local minima or maxima.
- Show that is an even function. What kind of symmetry would you expect its graph to display?
- Show that is an odd function. What kind of symmetry would you expect its graph to display?
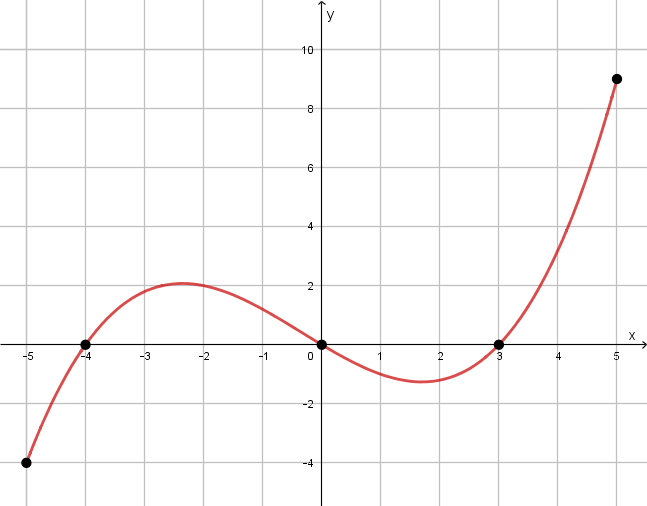
The graph of the function is shown below. Determine the domain and range of . Determine intervals on which and intervals on which . Determine open intervals on which is increasing/decreasing. Determine any local minima or maxima.