Section 4.2 - Exponential Functions

Section Objectives

1. Evaluate exponential functions.
2. Graph exponential functions.
3. Use exponential functions in applications.

Exponential Functions

Let $a$ be a fixed positive real number not equal to 1. The base-$a$ exponential function is defined by $f(x)=a^x$.

Examples

• Make a table of values for the function $f(x)=2^x$. Then sketch the graph. (Solution)

• Make a table of values for the function $\displaystyle f(x)=\left(\frac{1}{2}\right)^x = 2^{-x}$. Then sketch the graph. (Solution)

Properties of the Exponential Functions

In general, the exponential functions have the following properties.

$f(x)=a^x, a>1$

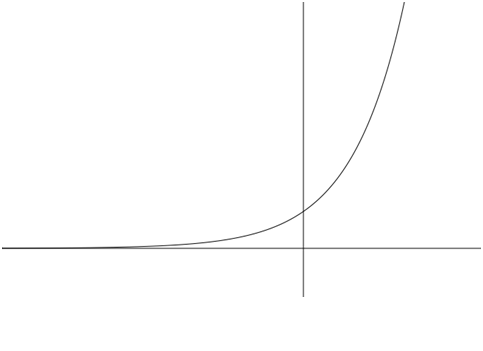
• Continuous and increasing
• One-to-one ( Graph passes the horizontal line test.)
• Domain: $(-\infty, +\infty)$, i.e., all real numbers
• Range: $(0,+\infty)$, i.e., all positive real numbers
• $y=0$ is a horizontal asymptote of the graph. In fact, $f(x) \to 0$ as $x \to -\infty$.
• $(0,1)$ is the $y$-intercept of the graph.
• $(1,a)$ is a point on the graph.
• $f(x) \to \infty$ as $x \to \infty$

$f(x)=a^x, 0<a<1$

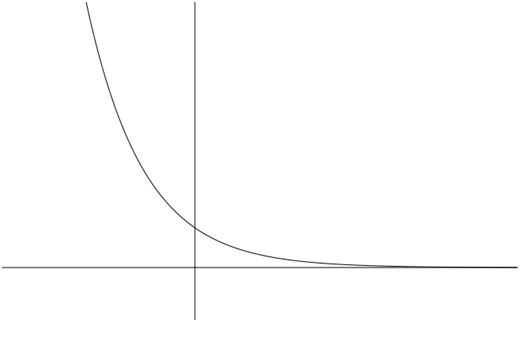
• Continuous and decreasing
• One-to-one ( Graph passes the horizontal line test.)
• Domain: $(-\infty, +\infty)$, i.e., all real numbers
• Range: $(0,+\infty)$, i.e., all positive real numbers
• $y=0$ is a horizontal asymptote of the graph. In fact, $f(x) \to 0$ as $x \to +\infty$.
• $(0,1)$ is the $y$-intercept of the graph.
• $(-1,1/a)$ is a point on the graph.
• $f(x) \to \infty$ as $x \to -\infty$

Examples

• Discuss the graph of $y=3^x$. (Solution)

• Discuss the graph of $y=(2/3)^x$. (Solution)

• Discuss the graph of $y=1+2^{x-3}$. (Solution)

Solving Elementary Exponential Equations

Equations involving exponential functions arise in many applications. Certain kinds of exponential equations, namely those involving exponentials of the same base, have a very simple solution method. The method is based on the fact that $a^x=a^y$ if and only if $x=y$.

In order to use this idea to solve an exponential equation,

1. Rewrite the equation so that a single term is on each side.
2. Write each side in terms of the same base.
3. Write the new equation that says the exponents are equal.
4. Solve the new equation.

Examples

• Solve $25^x-125=0$ (Solution)

• Solve $8^{r-1}=\frac{1}{2}$ (Solution)

• Solve $3^{2x-7} = 27^{x/2}$ (Solution)

The Base-$e$ Exponential

The number $e$ is a special mathematical constant that arises in many places in mathematics. This number is defined by the following limit: $(1+1/n)^n \to e$ as $n \to \infty$.

$e$ is an irrational number whose value is approximately $2.71828$.

$e$ is very often used as a base for an exponential function: $f(x)=e^x$. In fact, $e$ is usually called the "natural base".

Example

• Discuss the graphs of $y=e^x$ and $y=e^{-x}$. (Solution)

Applications - Population Growth

A very common population growth model is to assume that a population grows (or decays) according to a formula of the form $P(t)=P_0 a^t$, where $P_0=P(0)$, the initial population at time $t=0$, and the base $a$ is a number the characterizes the rate of growth (or decay). (In fact, $a-1$ is the growth rate per unit time.)

Example

• A biologist begins with 1000 bacteria, and the population doubles every hour. Find the formula of the form $P(t)=P_0 a^t$ that describes the growth of the bacteria culture. (Solution)

• In an effort to control vegetation overgrowth, 100 rabbits are released into an isolated area that is free of predators. After one year, the rabbit population has increased to 500. Assuming exponential population growth, what will the population be after another 6 months? (Solution)

VERY IMPORTANT IDEA: The model $P(t)=P_0 a^t$ describes growth if $a>1$, and it describes decay if $0<a<1$.

Applications - Compound Interest

An investment of $P$ dollars at an annual interest rate of $r$ compounded $n$ times per year has an accumulated value after $t$ years of $A(t)=P(1+r/n)^{nt}$.

If the interest is compounded continuously, $A(t)=Pe^rt$.

Example

• Sandy invests $10,000 in an account that earns 4.5% compounded quarterly. What is the value of the investment after 3.5 years? (Solution)

• What if interest is compounded continuously? (Solution)

Applications - Radioactive Decay

Radioactive decay is modeled by a formula identical to that of exponential population growth, except that the base $a$ is between 0 and 1: $P(t)=P_0 a^t$, $0<a<1$, where $P_0=P(0)$ is the initial amount of the radioactive substance.

The half-life of a radioactive isotope is the amount of time required for half of a given amount to decay. The half-life, $t_{1/2}$, satisfies the equation $\frac{1}{2} = a^{t_{1/2}}$.

If you know the half-life, this equation can be used to find the base $a$.

Example

• The half-life of Carbon-14 is 5728 years. Determine the base $a$ so that the formula $P(t)=P_0 a^t$ models the decay. (Solution)

• Polonium-210 has a half-life of 140 days. A scientist has 25 grams of Polonium-210. How many grams will remain after one year? (Solution)

For further help...

1. Problems involving exponential equations and exponential growth/decay can be very hard. Rather than look at random problems that are available on-line, you are probably best off just practicing ALEKS problems.
2. Ask for help when you got stuck.