Section 3.2 - Basic Rational & Power Functions and More Transformations
Section Objectives
- Develop a familiarity with the whole-number power functions and basic rational functions.
- Apply transformations to basic functions.
Intro to Polynomials and Rational Functions
An -th-degree polynomial in the variable is a function of the form
,
where the coefficients , , , are real or complex numbers with . We will be almost exclusively interested in polynomials with real coefficients.
Here are some examples of polynomial functions...
A rational function is a ratio of two polynomials. That is, a rational function is a function of the form
where and are polynomials and .
The domain of a rational function is the set of all real numbers for which the denominator is nonzero.
Here are some examples of rational functions...
Reciprocal functions
One of the simplest rational functions is the reciprocal function .
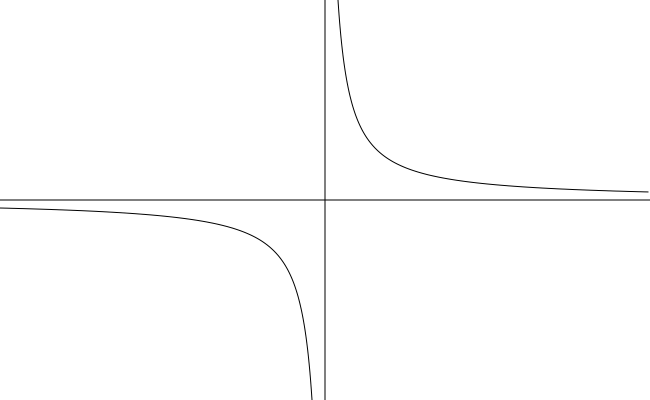
- Domain
- Range
- The reciprocal function is an odd function. Its graph is symmetric about the origin.
- As , . (The -axis is a horizontal asymptote of the graph.)
- As , . (The -axis is a vertical asymptote of the graph.)
Another of the simpler rational functions is the reciprocal square function .
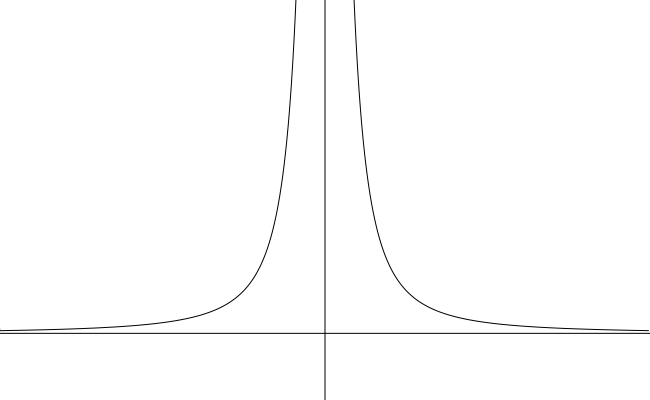
- Domain
- Range
- The reciprocal square function is an even function. Its graph is symmetric about the -axis.
- As , . (The -axis is a horizontal asymptote of the graph.)
- As , . (The -axis is a vertical asymptote of the graph.)
We have now added the reciprocal function and the reciprocal square function to our toolbox of common functions. Become familiar with these new functions!
Examples
- Sketch the graph of . Domain? Range? Asymptotic behavior? (Solution)
- Determine the horizontal and vertical asymptotes of the graph of . (Solution)
- Sketch the graph of . (Solution)
Even-number Power Functions: ,
The graphs of , , , ... are U-shaped curves opening upward with the turning point at the origin.

The bigger the exponent, the flatter the curve is on the interval and the steeper the curve is outside that interval.
Odd-number Power Functions: ,
The graphs of , , , ... have the following shape. Each has a flat spot at the origin.

The bigger the exponent, the flatter the curve is on the interval and the steeper the curve is outside that interval.
Examples
- Sketch a rough graph of . Domain? Range? End behavior? (Solution)
- Sketch a rough graph of . Domain? Range? End behavior? (Solution)
- The graph of is shifted downward by 7 units. Find an equation for the new graph. (Solution)
- Let .
(1) Describe the graph of .
(2) Find the graph's intercepts.
(3) Find the coordinates of the vertex.
(4) Find an equation for the symmetry axis. (Solution)
- Describe and sketch the graph of . (Solution)
For further help...
There are lots of resources available to help you with transformations.
- Do a Google search for "Transformations of functions".
- Here is a video posted by a colleague at UIC.
- Use Desmos or Geogebra to graph functions, and transform by sliding the graph.