Section 3.5 - Algebraic Operations on Functions
Section Objectives
- Compute sums, differences, products, and quotients of functions.
- Compute a composition of functions.
- Write a function as a composition of functions.
- Solve problems involving operations on functions.
Combining functions
Besides transforming individual functions, two or more functions can be combined in lots of ways to produce new functions.
The most basic combinations of functions come from the four basic arithmetic operations.
- , provided that
Examples
Given the following table of values, compute , , and . (Solution)
x f(x) g(x) 0 5 2 1 -3 7 2 10 -2 3 -8 -10
- Let and . Compute . What about ? (Solution)
- Sketch the graphs of and . Use the graphs to evaluate . What about ? (Solution)
Compositions
Another useful and important way of combining functions is to form the composition. Functions are composed when the output of one function is used as the input for a second function.
The composition of and , written , is the new function . In a composition of functions, the output of the first function is the input of the second.
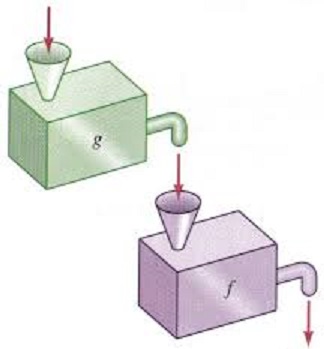
Examples
- Let and let . What function is ? What about ? What about ? (Solution)
- Refer to the table above. Compute . (Solution)
- Let . Find two functions and so that . (Solution)
- Let and . Find and determine its domain. (Solution)
- Let and . Find and completely simplify . What is the domain of the composition? (Solution)
- A large spherical balloon is being inflated so that its radius, in feet, after minutes is given by . Find its volume as function of . (Solution)
- An object is cooling in such a way that its temperature in degrees Celsius after minutes is given by . The formula is used to convert from temperatures in Celsius to Fahrenheit. Find the temperature of the object in degrees Fahrenheit at time . (Solution)
For further help...
- Do a Google search for "operations on functions" and/or "compositions of functions".
- Here is a video posted by a colleague at UIC.
- Do a Google search for "word problems with compositions of functions".