Section 4.1 - Quadratic Functions and Applications

Section Objectives

1. Find the vertex, intercepts, and symmetry axis of a parabola.
2. Write a quadratic function in vertex form.
3. Find the equation of a quadratic function from its graph.
4. Solve application problems involving quadratic functions and parabolas.

Quadratic functions

A quadratic function is a 2nd degree polynomial function. Every quadratic function can be written in the standard form $f(x)=ax^2+bx+c$, where $a$, $b$, and $c$ are real numbers with $a \ne 0$.

The graph of a quadratic function is a smooth U-shaped curve called a parabola. The turning point at the tip of the U is called the vertex, and the graph is symmetric about the vertical line through the vertex.

By completing the square, any quadratic function in standard form, $f(x) = ax^2+bx+c$, can be rewritten in the equivalent vertex form

$f(x) = a (x-h)^2 + k$.

• The vertex is at the point $(h,k)$, where $\displaystyle h=-\frac{b}{2a}$ and $k=f(h)$.
• The axis of symmetry is the vertical line $x=h$.
• The parabola opens upward if $a>0$ and downward if $a<0$ .
• The graph is wider than the graph of $y=x^2$ if $-1 \le a \le 1$ , as wide if $a=1$, and narrower if $|a|>1$.
• The $x$-intercepts of the graph can be found by solving $f(x)=0$ (i.e., finding the zeros of $f$). If a parabola has two distinct $x$-intercepts, the vertex is directly between them.
• The $y$-intercept is $(0,f(0))$.
• The quadratic function $f$ attains an extreme value (max or min) at the vertex of its graph.

Examples

• Consider the quadratic function defined by $f(x)=x^2+6x-7$. Find the $x$-intercepts of the graph, the coordinates of the vertex, and the axis of symmetry. Finally, write the equation in vertex form and sketch the graph. (Solution)

• Sketch the graph of $f(x)=-2(x-3)^2+4$. Describe the features of the graph/function. (Solution)

• A ball is thrown upward with a velocity of $48$ feet per second from the top of a $144$-foot building. What is the maximum height of the ball? How long until the ball hits the ground? (Solution) $h(t) = -16t^2 +48t+144$

• A quadratic function has a leading coefficient of $3$ and zeros $x=6$ and $x=-2$. Write its equation in standard form and vertex form. (Solution)

• The total cost of manufacturing a set of golf clubs is given by

  $$C(x) = 800 - 10x + 0.20x^2,$$

  where $x$ is the number of sets of golf clubs produced. How many sets of golf clubs should be manufactured to incur minimum cost and what is that minimum cost? (Solution)

• Cindy wants to construct two side-by-side dog-training pens of the same size and sharing one common side. She has 400 ft of fencing material to use. What values of $x$ and $y$ maximize the combined areas of the pens? (Solution)

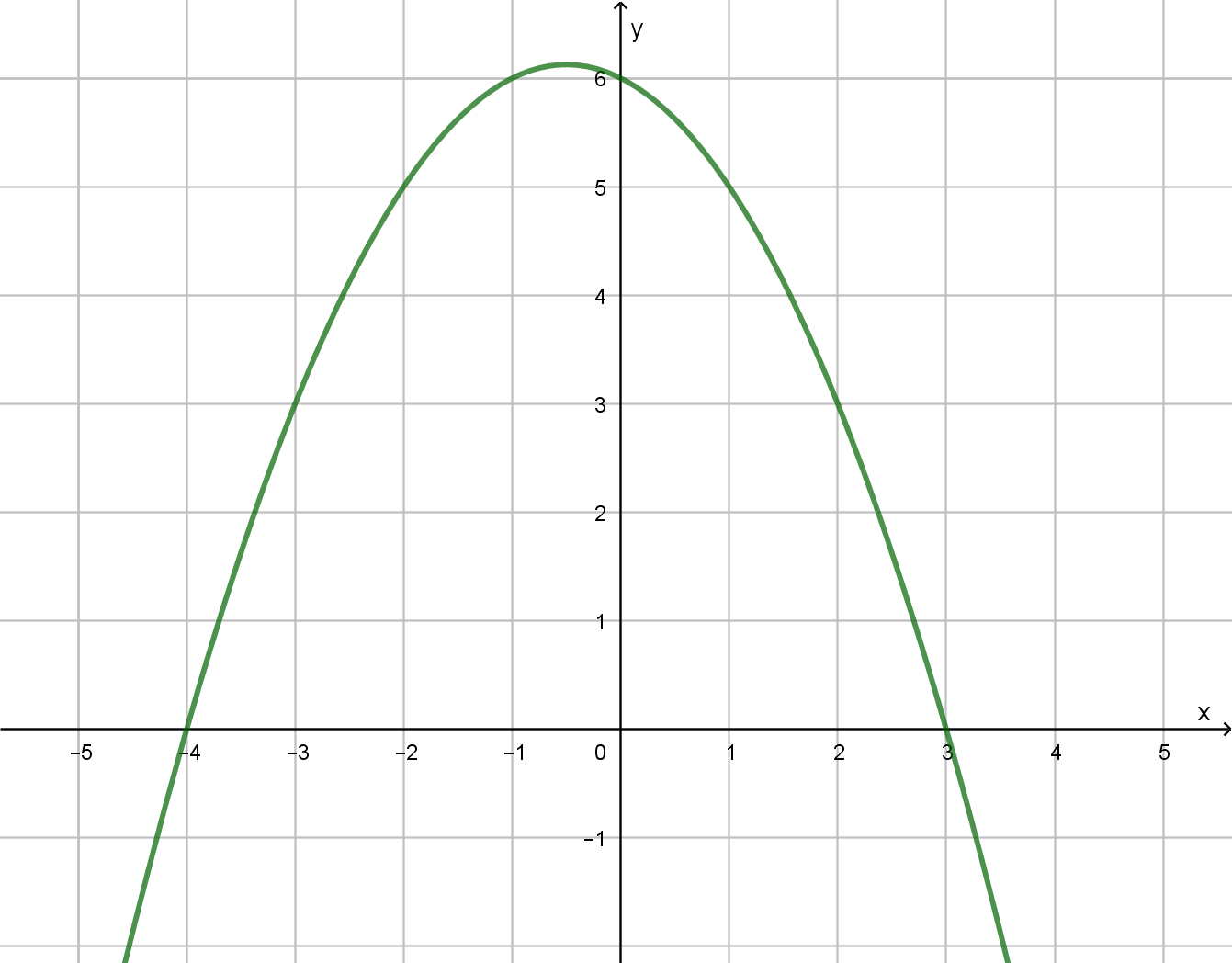
• The graph of a parabola is shown below. Find an equation for the graph. (Solution)

For further help...

There are lots of resources available to help you with transformations.

1. Do a Google search for "vertex form of parabola". Among other things, you will find some good Khan Academy videos.
2. Use Desmos or Geogebra to graph parabolas and find vertices & intercepts.
3. Do a Google search for "applications of quadratic functions".