Section 4.4 - Polynomials and Their Graphs

Section Objectives

1. Determine the end behavior of a polynomial function.
2. Use multiplicities of zeros and end behavior to graph a polynomial function.

End behavior, zeros, and polynomial graphs

Consider the polynomial $f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$, where the coefficients $a_n$, $a_{n-1}$, $\dots$, $a_0$ are real numbers with $a_n \ne 0$.

The general shape of the graph of $f$ can be easily determined from the polynomial's factored form.

• The graph crosses the $x$-axis at every zero of multiplicity 1.

• The graph flattens and crosses the $x$-axis at every zero of odd multiplicity.

• The graph flattens, touches, and bounces off the $x$-axis at every zero of even multiplicity.

• The end behavior (the behavior as $x \to \pm \infty$) of the graph of is identical to that of $y=a_nx^n$, where $n$ is the degree and $a_n$ is the leading coefficient:

  • $n$ even and $a_n$ positive $\longrightarrow$ up left and up right
  • $n$ even and $a_n$ negative $\longrightarrow$ down left and down right
  • $n$ odd and $a_n$ positive $\longrightarrow$ down left and up right
  • $n$ odd and $a_n$ negative $\longrightarrow$ up left and down right

Example

• Here is the graph of $f(x)=0.001(x-4)^3(x-1)(x+3)^2$. (Discussion)

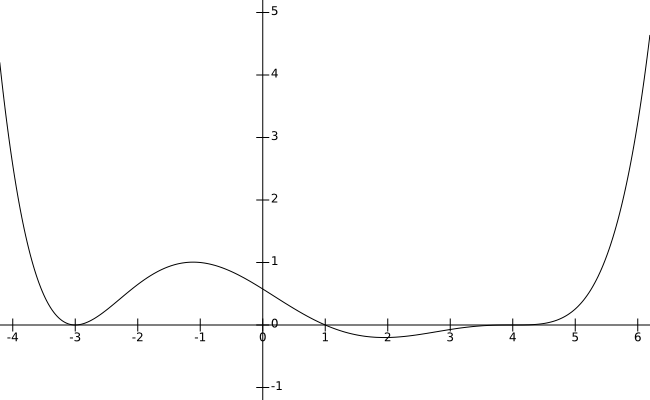
• Discuss the zeros and the features of the graph of $g(x)=x^2(x-3)^5$. (Solution)

• Imagine you were given the graph of a polynomial function, but you were not given the polynomial itself. Could you make good predictions about the zeros and their multiplicities? (Here are some examples from an old review packet: first and second.)

For further help...

1. Do a Google search for "graphing polynomials".
2. Video on zeros of polynomials.
3. Video on polynomial end behavior.
4. Use Desmos or Geogebra to graph polynomials.