 |
|
|
| Lg Square = x2 | Rectangle = x | Sm Square = 1 |
 |
|
|
| Lg Red Square = -x2 | Red Rectangle = -x | Sm Red Square = -1 |
Algebra
Tiles
Manipulatives and More
Algebra tiles are often used in the middle school classroom to illustrate operations on polynomials.
What are algebra tiles?
Algebra tiles are manipulatives with which you can represent polynomials and perform polynomial operations. Each tile represents a specific monomial.
 |
|
|
| Lg Square = x2 | Rectangle = x | Sm Square = 1 |
 |
|
|
| Lg Red Square = -x2 | Red Rectangle = -x | Sm Red Square = -1 |
To represent a 2nd degree polynomial, simply combine tiles. A red tile and a green tile of equal size will combine to give zero. Shown below is a representation of the polynomial 2x2 - x + 3.

Addition & Subtraction
Addition and subtraction are performed by combining or removing tiles. Once again, keep in mind that a green tile and a red tile of equal size cancel to leave zero. When subtracting you may need to use this idea in reverse and add zero to a polynomial. Try the following problems.
Multiplication
Multiplying polynomials using algebra tiles is a lot like using the array or area approach to multiplying whole numbers. Illustrated below is the multiplication fact (x-2)(x+1) = x2 - x - 2.
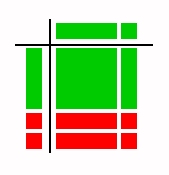
This figure actually shows that (x-2)(x+1) = x2 - 2x + x - 2. To make sure you've got it, try some of these problems.
(x+1)(x+1) (Notice that the resulting array forms a perfect square.)
(x+3)(x-2)
(2x+1)(x-2)
Factoring
To factor try to reverse the multiplying process. For example, to factor x2 - 3x + 2, arrange the appropriate tiles into a rectangular array and determine which factors would give this array.
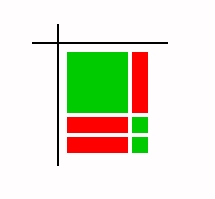 |
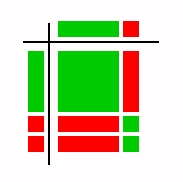 |
When factoring you may need to add some red and green tiles of equal size. Remember that you need to be able to make a rectangular array. If you can't make such an array, your polynomial can't be factored over the integers. Here are a few polynomials for you to factor.
Completing the Square
Algebra tiles can also be used to illustrate the process of completing the square. I'll leave this for you to figure out. A good example to start with is to show that x2 + 4x + 2 = (x + 2)2 - 2.
| Steve Kifowit Prairie State College Chicago Heights, IL 60411 |