Section 2.1 - Vectors in the plane

Section Objectives

1. Describe vectors in the plane, and write them in component form and in terms of basis vectors.
2. Compute the magnitude of a vector in 2-space.
3. Describe and perform basic operations on vectors in 2-space.

Intro to vectors

A vector is an abstract mathematical object used to describe a quantity that has both magnitude and direction.

Vectors are typically represented by directed line segments. The magnitude of the vector corresponds to the length of the line segment, and the direction of the vector corresponds to the direction of the line segment.

A vector is uniquely determined by its direction and its magnitude. If two vectors have the same direction and magnitude, they are equivalent (or equal). Vectors are not determined by their positions! (Here is an image showing several equivalent vectors.)

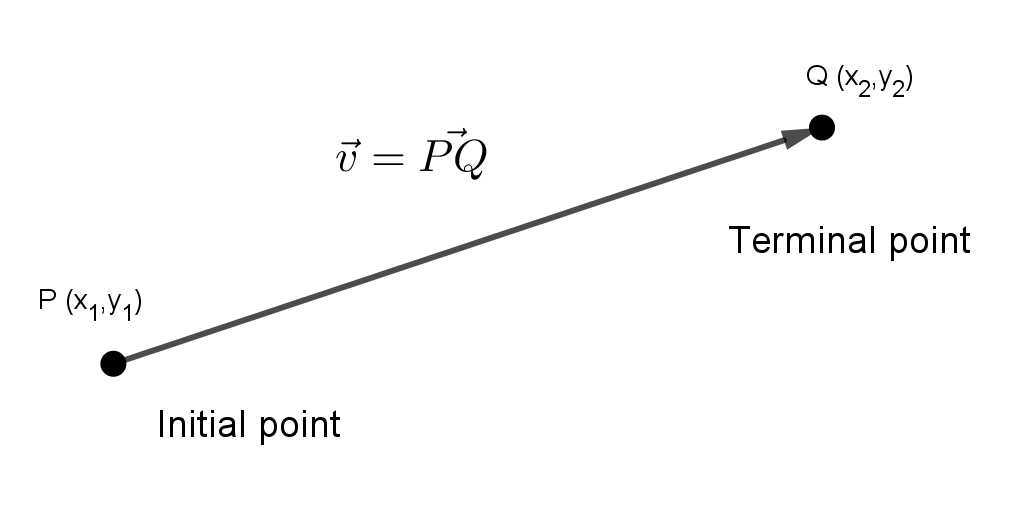
The component form of the vector $\vec{v}$ from $P\,(x_1,y_1)$ to $Q\,(x_2,y_2)$ is

A vector is in standard position when its initial point is the origin. A vector in standard position is uniquely determined by it terminal point. The component form of a vector simply describes the terminal point of the equivalent vector in standard position.

Examples

• Find the component form of the vector from $P\,(3,-4)$ to $Q\,(-2,-1)$. Sketch the vector and the equivalent vector in standard position.

• In component form, $\vec{v} = \langle -9,3 \rangle$. Find its initial point, $P$, if its terminal point is $Q\,(1,7)$.

Magnitude

The magnitude of a vector is the length of its corresponding directed line segment. When vectors are written in component form, their magnitudes are easy to compute (Pythagorean theorem or distance formula).

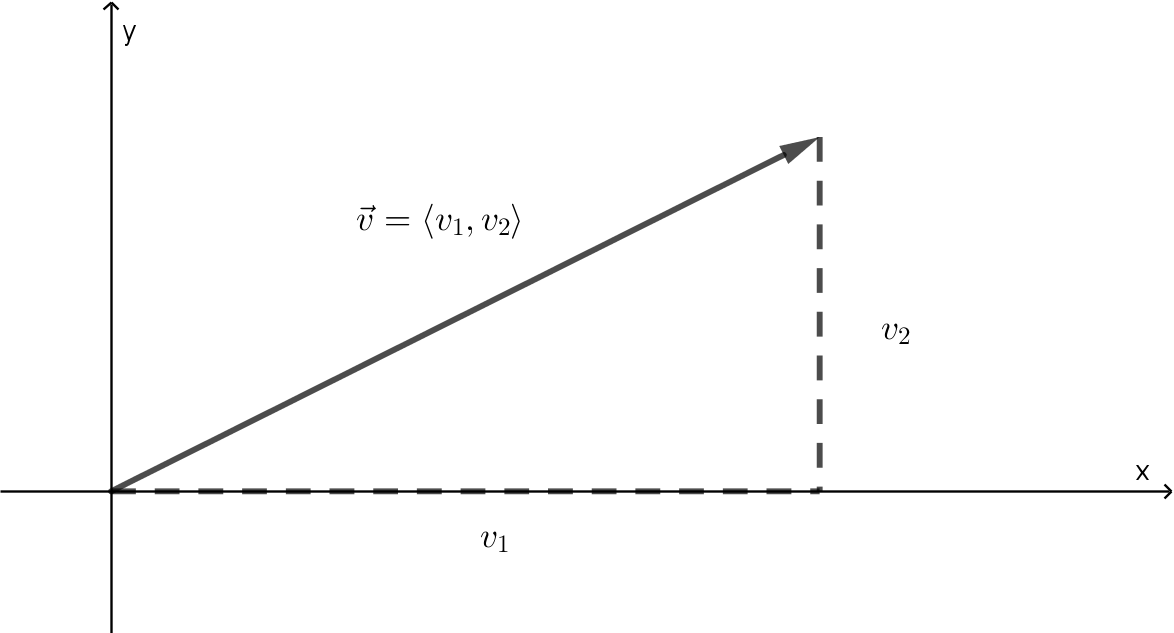
The magnitude of $\vec{v}$ is given by $\|\vec{v}\| = \sqrt{v_1^2+v_2^2}$.

Examples

• Find the magnitude of $\vec{PQ}$ if $P\,(-1,-3)$ and $Q\,(-2,7)$.

• The vector $\vec{u} = \langle \frac{3}{5}, -\frac{4}{5} \rangle$ is an example of a unit vector. Compute its magnitude.

Scalar multiplication/division

The product of the scalar $k$ and the vector $\vec{v}$, written $k\vec{v}$, is the new vector that has magnitude $|k|\,\|\vec{v}\|$ and whose direction is the same as or the opposite of the direction of $\vec{v}$ depending on the sign of $k$. This is called scalar multiplication. For vectors in component form, it follows that

Even though this looks like a distibutive property, it is not!

Examples

• Let $\vec{v}=\langle -2,1 \rangle$. Sketch the vectors $\vec{v}$, $2\vec{v}$, and $-\vec{v}$ and $-3\vec{v}$.

• To normalize a nonzero vector means to divide it by its magntiude. Equivalently, this mean to find a unit vector with the same direction as the original vector. Normalize the vector $\vec{w} = \langle -5,-12 \rangle$.

• Find a vector of magnitude $17$ that has the direction of $\vec{z}=\langle 4,-9 \rangle$.

Additon and subtraction of vectors

The two vectors $\vec{u}$ and $\vec{v}$ can be added by using the terminal point of $\vec{u}$ as the initial point of $\vec{v}$. See the figure below.

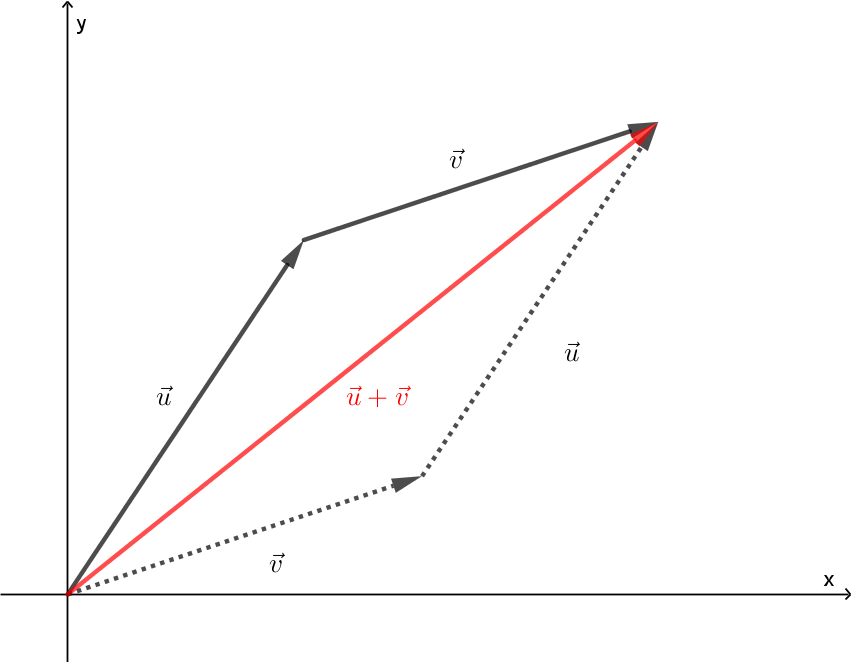
You can think about addition by the triangle method or the parallelogram method. In any case, it should be clear that in component form, we have

Perhaps the best way to think about vector subtraction is to consider that $\vec{u}-\vec{v}$ should answer the question, "What plus $\vec{v}$ is $\vec{u}$?"

It should also be pretty clear in this case that

Examples

• Sketch the vectors $\vec{v}=\langle 1, -2 \rangle$ and $\vec{w}=\langle -4, -3 \rangle$. Then sketch and compute the vectors $\vec{v}+\vec{w}$, $\vec{v}-\vec{w}$, and $\vec{w}-\vec{v}$.

• Let $\vec{x}=\langle 3,-9 \rangle$ and $\vec{y}=\langle -5,6 \rangle$. Compute $-2\vec{x}+3\vec{y}$.

Properties of vector operations

For any vectors $\vec{u}$, $\vec{v}$, and $\vec{w}$, and scalars $r$ and $s$, the following properties hold:

1. $\vec{u}+\vec{v}=\vec{v}+\vec{u}$
2. $(\vec{u}+\vec{v})+\vec{w} = \vec{u} + (\vec{v}+\vec{w})$
3. There exists a vector $\vec{0}$ such that $\vec{u}+\vec{0}=\vec{u}$.
4. $\vec{u}+(-\vec{u})=\vec{0}$
5. $r(s\vec{u})=(rs)\vec{u}$
6. $(r+s)\vec{u}=r\vec{u}+s\vec{u}$
7. $r(\vec{u}+\vec{v})=r\vec{u}+r\vec{v}$
8. $1\vec{u}=\vec{u} \quad$ and $\quad 0\vec{u}=\vec{0}$

These properties are pretty easy to prove. But perhaps what is more interesting is that these properties can also hold for more abstract objects. In fact, any collection of "objects" that satisfy these properties is called a vector space. You will study general vector spaces in a Linear Algebra class.

Basis vectors

In addition to writing write vectors in component form, it is often convenient (and useful) to write vectors in terms of other vectors. For now, the most convenient "other" vectors are the unit vectors $\hat{\imath}$ and $\hat{\jmath}$:

Any vector in component form can easily be written in terms of these basis vectors $\hat{\imath}$ and $\hat{\jmath}$. For example,

From this point forward, we will call either form, $\langle 5,9 \rangle$ or $5\hat{\imath}+9\hat{\jmath}$, component form since each form explicitly shows the components.

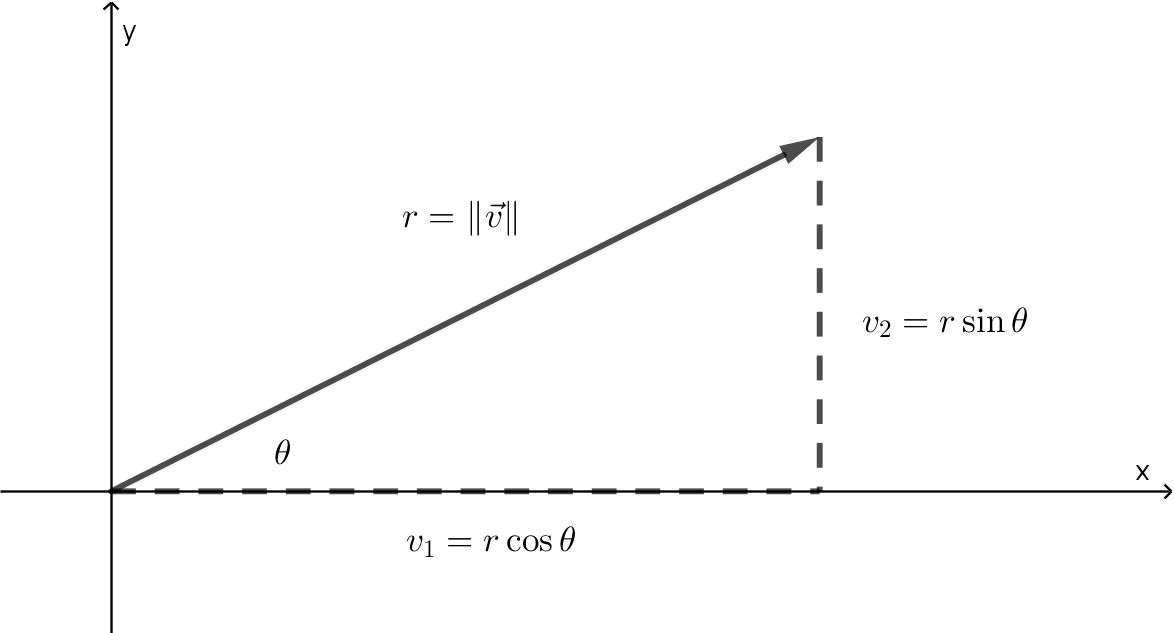
Here is one last important idea before we close this section. Any vector in 2-space can be written in terms of its magnitude and the angle it makes with the positive $x$-axis. Indeed, if $\vec{v}$ has magnitude $r$ and makes an angle $\theta$ with the positive $x$-axis, then it follows from trigonometry that

as you can see from the figure below.

Examples

• Determine a unit vector that makes a $60^{\circ}$ angle with the positive $x$-axis.

• What angle does the vector $\vec{z}=-3\hat{\imath}-5\hat{\jmath}$ make with the positive $x$-axis?

• Determine a vector of magnitude $7$ is that perpendicular to $\vec{w}=-4\hat{\imath}+2\hat{\jmath}$.