Section 2.3 - The dot product

Section Objectives

1. Compute the dot product of two vectors.
2. Find and use the projection of one vector onto another.
3. Find the direction cosines of a vector.
4. Use the dot product in applications involving orthogonality, work, angles between vectors, projections, etc.

The dot product

There are several possible ways that we could define the product of two vectors. In fact, we will study two such ways in great detail. The first is the dot product. The dot product of two vectors is the scalar product denoted by a centered dot and defined as follows:

If you have ever multiplied matrices, you might recognize the dot product as the product of a 1-by-3 matrix and a 3-by-1 matrix. This may seem like an unusual way to combine vectors, but we will soon see otherwise.

Examples

• Let $\vec{v}=-\hat{\imath}+3\hat{\jmath}-5\hat{k}$ and $\vec{w}=4\hat{\imath}+2\hat{\jmath}+3\hat{k}$. Compute $\vec{v} \cdot \vec{w}$ and $\vec{w} \cdot \vec{v}$.

• Let $\vec{w} = 2\hat{\imath}+5\hat{\jmath}-\hat{k}$. Find a unit vector $\vec{u}$ with the property that $\vec{u} \cdot \vec{w} =0$.

Properties of the dot product

The following properties hold for any vectors $\vec{u}$, $\vec{v}$, and $\vec{w}$ and scalar $c$.

1. $\vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}$
2. $\vec{u} \cdot (\vec{v}+\vec{w}) = \vec{u} \cdot \vec{v} + \vec{u} \cdot \vec{w}$
3. $c(\vec{u} \cdot \vec{v}) = (c\vec{u}) \cdot \vec{v} = \vec{u} \cdot (c\vec{v})$
4. $\vec{v} \cdot \vec{v} = \|\vec{v}\|^2$

These properties of the dot product are pretty easy to prove. The fourth property will be one we use quite often.

The dot product and the angle between vectors

The dot product has an alternative formula that relates it to the angle between the vectors:

where $\theta$ is the angle between $\vec{u}$ and $\vec{v}$. (Typically we restrict $\theta$ so that $0 \le \theta \le \pi$).

This formula follows from the Law of Cosines, which you studied in your trigonometry class. A few important ideas should be clear from this formula:

For nonzero vectors $\vec{u}$ and $\vec{v}$,

1. $\theta$ is a right angle if and only if $\vec{u} \cdot \vec{v}=0$.
2. $\theta$ is obtuse if and only if $\vec{u} \cdot \vec{v} <0$.
3. $\theta$ is acute if and only if $\vec{u} \cdot \vec{v} >0$.

Examples

• Consider the points $A\,(1,1,2)$, $B\,(3,6,8)$, and $C\,(-1,-3,6)$. Show that triangle $ABC$ is a right triangle with its right angle at $A$.

• Determine the angle between the vectors $\vec{a}=\hat{\imath}+\hat{\jmath}+\hat{k}$ and $\vec{b}=2\hat{\imath}-\hat{\jmath}-3\hat{k}$.

• Two vectors are orthogonal if their dot product is zero. What does this say about the vectors from a geometrical point of view? Find a vector orthogonal to $\vec{r} = \langle 3,-4,2 \rangle$.

Projections

In applications of vectors, we are sometimes only interested in certain "parts" of vectors. For example, if you are applying a force to move a box along the floor, you might only be interested in the part of the force that is in the direction of the box's displacement. That "part" is a projection.

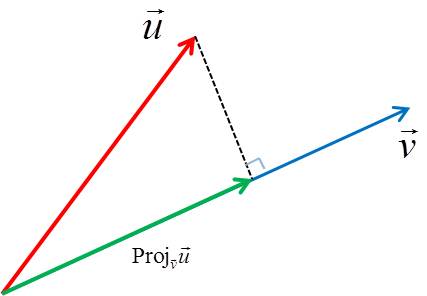
The vector projection of $\vec{u}$ onto $\vec{v}$ is given by

Unless we say otherwise, we will use the single word projection to refer to the vector projection. Notice that the projection has the direction of the vector that is being projected onto. In our notation, that's the vector we use as the subscript.

The scalar projection of $\vec{u}$ onto $\vec{v}$ is the signed length of the vector projection: $\displaystyle \frac{\vec{u} \cdot \vec{v}}{\|\vec{v}\|}$. This is also called the component of $\vec{u}$ in the direction of $\vec{v}$.

Examples

• Determine the projection of $\vec{x}=3\hat{\imath}+4\hat{\jmath}-5\hat{k}$ onto $\vec{y}=-2\hat{\imath}-2\hat{\jmath}+3\hat{k}$. Follow-up: What is the component of $\vec{x}$ in the direction of $\vec{y}\,$?

• Using the results from above, let $\vec{z} = \vec{x} - \mbox{proj}_{\vec{y}} \, \vec{x}$. Show that $\mbox{proj}_{\vec{y}} \, \vec{x}$ and $\vec{z}$ are orthogonal. (In this example, there is nothing special about the vectors $\vec{x}$ and $\vec{y}$. This result is always true.)

• If two nonzero vectors are orthogonal, what can you say about the projection of one onto the other?

• The work done by the force $\vec{F}$ to cause the displacement $\vec{d}$ is given by $\| \mbox{proj}_{\vec{d}} \, \vec{F} \| \, \| \vec{d} \|$. Show that this is equivalent to $\vec{F} \cdot \vec{d}$.

Direction cosines

Recall that a vector in 2-space can be written in terms of its magnitude and the angle it makes with the positive $x$-axis. At first glance, this idea does not generalize to vectors in 3-space, but it does if we think about it in the right way.

Notice that (by simply computing the dot products)

and that each component satisfies (by the alternative form of the dot product)

where $\alpha$, $\beta$, and $\gamma$ are the angles between $\vec{v}$ and the coordinate axes. It follows that

The angles $\alpha$, $\beta$, and $\gamma$ are called the direction angles for $\vec{v}$, and their cosines are called the direction cosines. An important consequence of this idea that the components of any unit vector are necessarily its direction cosines.

• Suppose $\vec{w}$ is the vector in 2-space with magnitude $r$ making the angles $\alpha$ and $\beta$ with the positive $x$- and $y$-axes, respectively. Show that $\vec{w}=r\cos \alpha \, \hat{\imath} + r \sin \alpha \, \hat{\jmath} = r\cos \alpha \, \hat{\imath} + r \cos \beta \, \hat{\jmath}$.

• Use direction cosines to determine the angles that $\vec{v}=\langle 2,3,3 \rangle$ makes with the coordinate axes. (Start by normalizing $\vec{v}$.)