Section 2.5 - Lines and planes in space

Section Objectives

1. Find parametric or symmetric equations for a line in space.
2. Find the equation of a plane in space.
3. Find the distance from a point to a line.
4. Find the distance from a point to a plane.
5. Find the angle between two planes.

Lines in space

In this section, we will use our knowledge of vectors to help us describe and work with lines and planes in 3-dimensional space. Let's start with lines.

Consider the line in space that passes through the point $P\,(x_0,y_0,z_0)$ and is parallel to the vector $\vec{v}=a\hat{\imath}+b\hat{\jmath}+c\hat{k}$. Let $Q\,(x,y,z)$ be another point on the line.

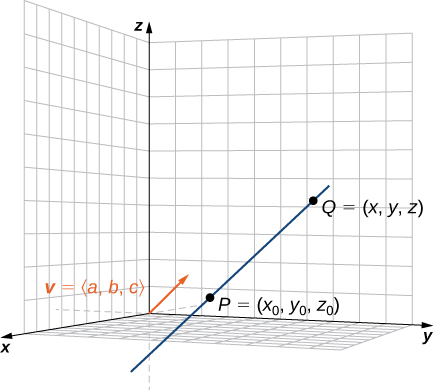
The vector $\vec{PQ} = (x-x_0) \hat{\imath} + (y-y_0) \hat{\jmath}+(z-z_0)\hat{k}$ must be parallel to $\vec{v}$. Therefore $\vec{PQ}=t\vec{v}$, for some scalar $t$. It follows that

or

These equations are the parametric equations for the line. If we solve each for $t$, we find the symmetric equations for the line:

In the symmetric equations, if one of the direction numbers ($a$, $b$, or $c$) is zero, then the corresponding fraction is not defined. In such a case, we will not write that fraction as part of the symmetric equations, rather we will simply write of value of the coordinate in its place. For example, parametric equations for the line through $(5,3,-7)$ and parallel to $\vec{v}=\langle 8,0,-4 \rangle$ are

and we will write the symmetric equations as

Examples

• Find parametric and symmetric equations for the line through $(3,-2,6)$ and parallel to $\langle -1,7,-4 \rangle$.

• Find a set of parametric equations for the line through $P\,(1,2,3)$ and $Q\,(4,8,1)$. What if we were only interested in the line segment $PQ$ but not the entire line?

Planes in space

To describe a plane in space, let's suppose we are given a point $P\,(x_0,y_0,z_0)$ on the plane and a vector $\vec{n}$ that is normal (perpendicular) to the plane. Then the plane is the collections of all points $Q\,(x,y,z)$ such that $\vec{PQ}$ is orthogonal to $\vec{n}$.

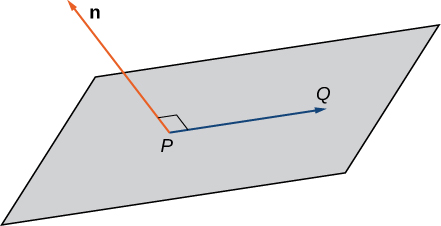
In other words,

This vector equation can be expanded by writing the vectors in component form and computing the dot product:

or

If we further expand the equation, we get the general form of the equation of a plane:

where $d=-ax_0-by_0-cz_0$.

Examples

• Find an equation of the plane that passes through $(4,2,1)$ and has normal vector $\vec{n}=\hat{\imath} - \hat{\jmath}+2 \hat{k}$.

• Find an equation of the plane that passes through the points $A\,(1,1,-1)$, $B\,(3,-5,3)$, and $C\,(-1,5,4)$.

• Find an equation of the plane that passes through $P\,(1,4,3)$ and contains the line given by $\displaystyle x=\frac{y-1}{2}=z+1$.

• The angle between two planes is the acute angle between the normal lines. We can use the normal vectors and the dot product to get that angle: $\displaystyle \cos \theta = \frac{|\vec{n_1} \cdot \vec{n_2}|}{\|\vec{n_1}\| \, \|\vec{n_2}\|}$. Find the angle between the planes given by $3x+2y-z=2$ and $x-2y-3z=6$.

• Find a set of parametric equations for the line of intersection of the planes in the example above. (Hint: The line has the direction of $\vec{n_1} \times \vec{n_2}$).

Distance from point to plane

Suppose $P\,(x_0,y_0,z_0)$ is a point on the plane $ax+by+cz+d=0$, which has normal vector $\langle a,b,c \rangle$. Also suppose that $Q\,(x_1,y_1,z_1)$ is a point that is not on the plane. Then the distance from the plane to the point is given by $D=\|\mbox{prog}_{\vec{n}} \, \vec{PQ} \|$ (see the figure).

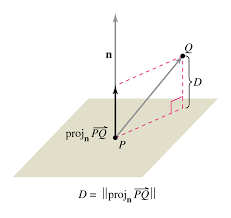
Is it easy to find a more convenient formula for $D$ by using the formula for the projection:

Now let's use the fact that $P$ satisfies that equation of the plane to say that

or

Therefore we have the following point-to-plane distance formula:

Examples

• Find the distance from the plane $2x+3y-6z=-5$ to the point $(3,2,-1)$.

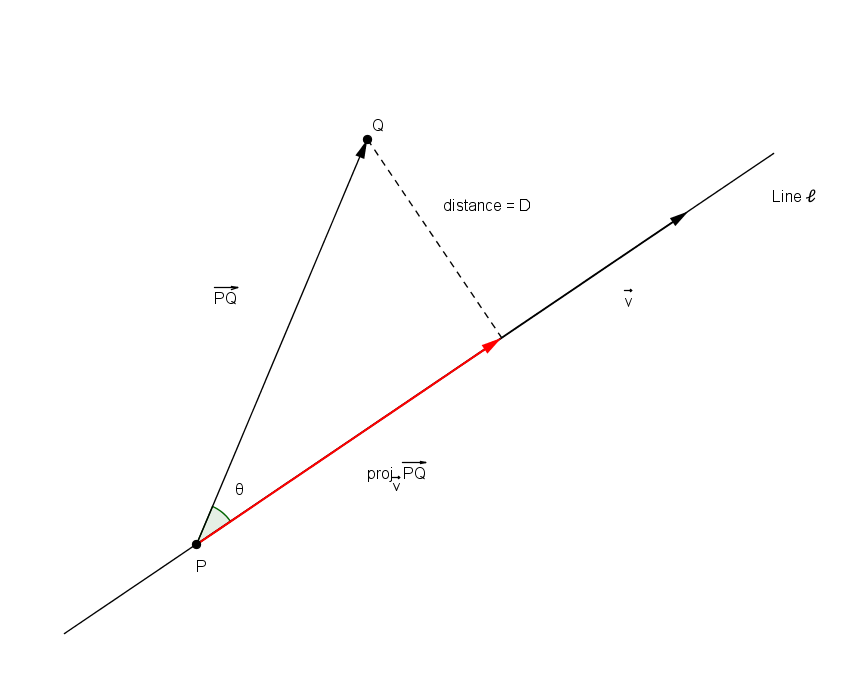
Distance from point to line

Suppose $P$ is a point on the line parallel to $\vec{v}$, and $Q$ is a point not on the line. By referring to the figure below, it is easy to derive the following point-to-line distance formula:

Examples

• Find the distance from the point $(2,-1,0)$ to the line described by $\displaystyle \frac{x-3}{2}=\frac{y-1}{3}=\frac{z+3}{6}$.