Section 2.6 - Cylinders and Quadric Surfaces

Section Objectives

1. Identify cylinders as 3-dimensional surfaces.
2. Recognize quadric surfaces from their graphs or equations.
3. Roughly sketch the graph of a quadric surface.
4. Sketch the traces of a quadric surface.

Cylinders

In the last section, we study planes, which are surfaces in space. In this section, we will continue our study of 3-dimensional surfaces. We are already somewhat familiar with the surfaces we call cylinders--think of a soda can or a can of vegetables. Actually, cylinders are far more general than these examples seem to indicate.

A cylinder is the set of all lines in space that are parallel to a given line and pass through a given curve. The curve is called the generating curve, and the parallel lines are called rulings.

In the following image, the generating curve is a circle in the $xy$-plane and the rulings are lines through the circle and parallel to the $z$-axis.

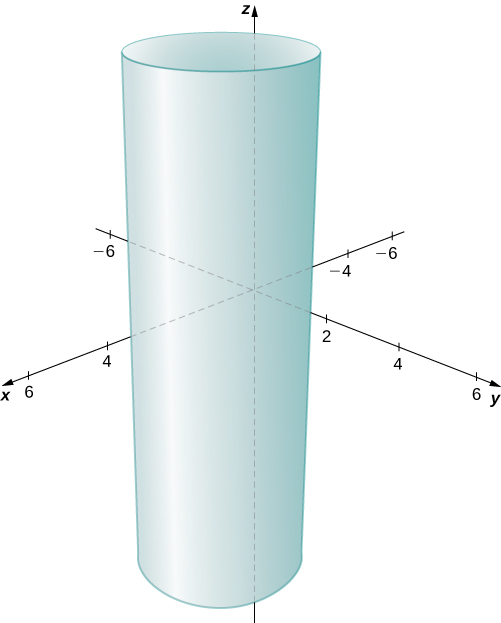
The generating curves are not required to be closed curves. For example, think about the parabola $y=x^2$ in the $xy$-plane. Now draw lines parallel to the $z$-axis through the parabola. The resulting surface is a cyclinder. You can easily construct this kind of surface with a sheet of paper.

When we consider the equation $y=x^2$ in 3-dimensional space, we notice immediately that we are "missing" the $z$-coordinates. This means the $z$-coordinates are arbitrary, and the equation $y=x^2$ defines the cylinder described above.

When considered in 3-dimensional space, any equation containing 2 out of the 3 rectangular coordinates describes a cylinder with the rulings parallel to the axis of the missing variable. This is not the only way to form cylinders, but it's an important way!

Examples

• Sketch or describe the surface given by $x^2+z^2=25$. (The rulings are lines parallel to the $y$-axis.)

• Sketch or describe the surface given by $y=\sin x$. (The rulings are lines parallel to the $z$-axis.)

• Use a computer graphing utility to sketch the graph of $z=2x^2-y$. It may not be immediately clear that this equation defines a cylinder, but it does. The generating curve is $y=2x^2$, and the rulings are lines that are parallel to the line $z+y=0$ in the $yz$-plane. Here is the SageMath code:

var("x,y")
plot3d(2*x^2-y, (x,-3,3), (y,-6,6), mesh=True) 

Traces of a surface

The traces of a surface are the cross-section curves created when the surface intersects a plane parallel to one of the coordinate axes. Depending on the context, we may also use the names contours, level curves, or cross sections when referring to traces. You can obtain an equation for a trace by fixing the level of one of the variables.

Examples

• Discuss the traces of the surfaces in the examples above.

Quadric surfaces

The quadric surfaces are the three-dimensional analogs of the conic sections. Recall that the conic sections are the ellipses (and circles), parabolas, and hyperbolas. (For a brief review of the conic sections, see chapter 12 of the OpenStax trig book.)

The quadric surfaces are the graphs of equations that can be written in the form

There are six types of quadric surfaces: ellipsoids (including spheres), paraboloids, cones, hyperboloids of one sheet, hyperboloids of two sheets, and hyperbolic paraboloids. We will only consider the quadric surfaces whose equations have no mixed-variable terms (i.e., $D=E=F=0$). In general, such terms can be eliminated by rotation of axes.

The quadric surfaces can be identified (and sketched) from their equations by thinking about their traces. For example, consider the equation $x^2+4y^2+z^2=4$. Fixing the value of the variable $z=c$, and therefore generating the trace at the "level" $z=c$, gives $x^2+4y^2=4-c^2$. This equation makes sense only when $-2 \le c \le 2$, and for each such $c$, the trace is an ellipse (at the level $z=c$). Similarly, fixing the value $y=c$ generates the circles $x^2+z^2=4-4c^2$ at the levels $y=c$ for $-1\le c \le 1$. Finally, fixing the value $x=c$ generates the ellipses $4y^2+z^2=4-c^2$ at the levels $x=c$ for $-2\le c \le2$. The traces or cross sections, which are all parallel to the coordinates planes, are either circles or ellipses. Our conclusion is that the original equation, $x^2+4y^2+z^2=4$, describes an ellipsoid. Whichever axis you look along, you will see circles or ellipses. Here is the SageMath code that will generate the ellipsoid:

xxxxxxxxxx
var("x,y,z")
implicit_plot3d(x^2+4*y^2+z^2==4, (x,-2,2), (y,-1,1), (z,-2,2))

Examples

• Identify and describe the graph of $\displaystyle x^2+\frac{y^2}{4}=z$.

xxxxxxxxxx
var("x,y,z")
implicit_plot3d(x^2+y^2/4==z, (x,-5,5), (y,-4,4), (z,0,4))

• Identify and describe the graph of $-4x^2+25y^2+z^2=100$.

xxxxxxxxxx
var("x,y,z")
implicit_plot3d(-4*x^2+25*y^2+z^2==100, (x,-10,10), (y,-12,12), (z,-20,20))

• Identify and describe the graph of $-x^2+2y^2-z^2=10$.

xxxxxxxxxx
var("x,y,z")
implicit_plot3d(-x^2+2*y^2-z^2==10, (x,-15,15), (y,-10,10), (z,-15,15))

• Identify and describe the graph of $5y=x^2-z^2$.

xxxxxxxxxx
var("x,y,z")
implicit_plot3d(5*y==x^2-z^2, (x,-15,15), (y,-10,10), (z,-15,15))

• Identify and describe the graph of $4x^2+y^2-z^2=0$.

xxxxxxxxxx
var("x,y,z")
implicit_plot3d(4*x^2+y^2-z^2==0, (x,-5,5), (y,-5,5), (z,-5,5))