Sections 7.3 & 7.4 - The Trig Functions on the Unit Circle
Section Objectives
- Define and evaluate the trigonometric functions on the unit circle.
- Use reference angles to evaluate the trigonometric functions.
- Recognize and use the even/odd properties of the trigonometric functions.
Sine and Cosine on the Unit Circle
The unit circle is described by the equation . Any point on the unit circle satisfies this equation.
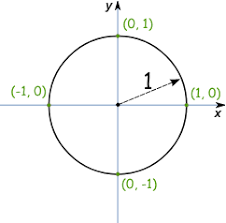
Let be any real number. Imagine starting at the point on the unit circle and traveling along the circle through an arc length of units (counterclockwise if is positive, clockwise if is negative). Notice that is the radian measure of the angle through which you've turned!
Now let be the point at which you arrived. The sine and cosine of the real number are defined as follows:
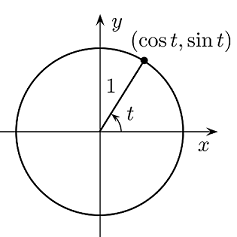
Do you remember discussing the Pythagorean identity . The unit circle approach reinforces this idea.
Examples
Use your unit circle to find the sine and cosine of .
Use your unit circle to find and .
The Other Trig Functions
The other trigonometric functions are the tangent, secant, cosecant, and cotangent. They can be defined in terms of the sine and cosine (as we saw with the right triangle approach).
The exact values of the trigonometric functions at certain special angles (multiples of and ) should be memorized! For now, we can read them off our unit circles.
Examples
Use your unit circle to find .
Use your unit circle to determine an angle for which is not defined.
Suppose is an angle in the 2nd quadrant and . Find the values of the other five trigonometric functions at .
Domains of the Trigonometric Functions
Notice that the sine and cosine functions are defined for all real numbers---there was no restriction on the real number .
On the other hand, the outputs of the sine and cosine functions are the coordinates of points on the unit circle. Therefore,
for all real numbers .
The sine and cosine functions take, as inputs, any real numbers, and they return, as outputs, real numbers between -1 and 1.
Based on the reciprocal definitions of the other trigonometric functions, the domains and ranges of the tangent, cotangent, secant, and cosecant functions can be determined.
Examples
Discuss the domain and range of the tangent function.
Discuss the domain and range of the cosecant function.
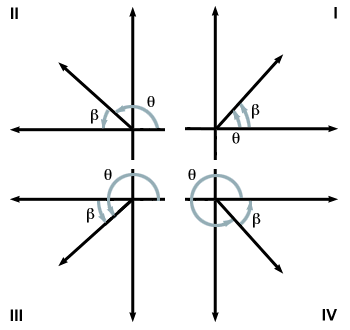
Reference Angles
Let be an angle in standard position. Its reference angle is the acute angle formed by the terminal side of and the horizontal axis.
Examples
Find the reference angle for .
Find the reference angle for .
Find the reference angle for .
Signs of the Trig Functions in the Quadrants
Based on our unit circle definitions of the trig functions, the following chart should be pretty clear. And these ideas are worth getting used to!

Evaluating the Trig Functions at any Angle
To evaluate a trigonometric function at any angle :
- Determine the reference angle for . Let's call it .
- Evaluate the trig function at .
- Depending on the quadrant in which lies, give the appropriate sign to the value you found in step 2.
Examples
Evaluate .
Evaluate .
Even/Odd Properties
Based on the unit circle and reference angles, the following symmetry properties are somewhat obvious.
The cosine and the secant are even functions:
The sine, cosecant, tangent, and cotangent are odd functions:
These properties can be quite useful when evaluating and simplifying trigonometric expressions.